Nya Gyidie

Nya Gyidie means "have faith". It is the symbol of faith.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

The plan to draw this shape is given below:

1. Lift up the pen
2. Set the pensize to 40
3. Draw the large circle
4. Set the pensize to 1
5. Draw the outer circles
6. Draw the inner square
7. Draw the supporting shape

Using Turtle Graphics

We will use the template.py file and rename it to nya.py.

The for the first two lines is shown below:

turtle.penup()

turtle.pensize(40)

To draw the large circle we need to move the turtle to the position (120, 0) and draw a circle of radius 120 pixels.

The code to do this is shown below:

turtle.setposition(120, 0)

turtle.setheading(90)

turtle.pendown()

turtle.circle(120)

The image generated is shown below:

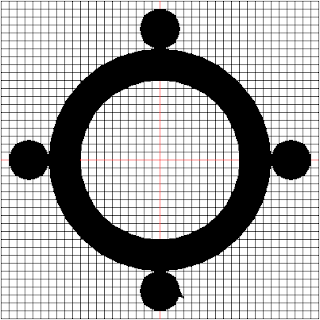
To draw the outer circles we need to get the coordinates of the right most sides of the circles.

Starting from the right and moving anticlockwise, they are (190, 0), (25, 165), (-140, 0) and (25, -165).

The code to draw the outer circles is shown below:

turtle.pensize(1)

turtle.penup()

turtle.begin_fill()

turtle.setposition(190, 0)

turtle.setheading(90)

turtle.pendown()

turtle.circle(25)

turtle.end_fill()

turtle.penup()

turtle.begin_fill()

turtle.setposition(25, 165)

turtle.setheading(90)

turtle.pendown()

turtle.circle(25)

turtle.end_fill()

turtle.penup()

turtle.begin_fill()

turtle.setposition(-140, 0)

turtle.setheading(90)

turtle.pendown()

turtle.circle(25)

turtle.end_fill()

turtle.penup()

turtle.begin_fill()

turtle.setposition(25, -165)

turtle.setheading(90)

turtle.pendown()

turtle.circle(25)

turtle.end_fill()

The generated image is shown below:

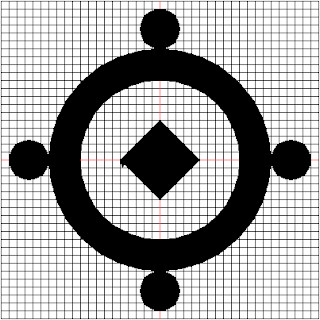
To draw the inner square, we need to move our turtle to the leftmost part of the square and find the angle as well as the length of the side.

The coordinate for the leftmost side is (-50, 0) while the coordinate for the uppermost part is (0, 50).

The code to find the angle between the two points is shown below:

myradians = math.atan2(50 - (0), 0 - (-50))

angle = math.degrees(myradians)

To find the length between the two sides, we need to use the coordinateDistance function. The code for it is shown below:

def coordinateDistance(x1, y1, x2, y2):

    dx = x1 - x2

    dy = y1 - y2

    D = math.sqrt((dx * dx) + (dy * dy))

    return D

We call the function using the code shown below:

length = coordinateDistance(-50, 0, 0, 50)

The code to draw the square is shown below:

turtle.penup()

turtle.setposition(-50, 0)

turtle.begin_fill()

turtle.pendown()

turtle.setheading(angle)

turtle.forward(length)

turtle.setheading(360 - angle)

turtle.forward(length)

turtle.setheading(180 + angle)

turtle.forward(length)

turtle.setheading(90 + angle)

turtle.forward(length)

turtle.end_fill()

The generated image is shown below:

Drawing the upper filled quadrant is not difficult. The quadrant starts at (-40, 90) and heads to the point (0, 50) where it joins the upper tip of the inner square.

To draw this quadrant we move the pen to the position (-40, 90) and draw a line to the point (0, 50). Then we draw the line back to the point (40, 90) where the quadrant ends. The fill property of Python turtle will fill the quadrant for us.

The code to do this is shown below:

turtle.setposition(-40, 90)

turtle.pendown()

turtle.begin_fill()

turtle.setheading(inclineAngle)

turtle.forward(inclineLength)

turtle.setheading(360 - inclineAngle)

turtle.forward(inclineLength)

turtle.end_fill()

The generated image is shown below:

To draw the lower filled quadrant, we need to use the same principles we use to draw the top quadrant.

The code for this is shown below:

turtle.penup()

turtle.setposition(-40, -90)

turtle.pendown()

turtle.begin_fill()

turtle.setheading(360 - inclineAngle)

turtle.forward(inclineLength)

turtle.setheading(360 + inclineAngle)

turtle.forward(inclineLength)

turtle.end_fill()

The generated image is shown below:

To close the gaps in the shape we need to use the fill property.

Move the turtle back to the position of the right hand of the upper triangle. Set the heading to 90 degrees and move forward by 10 pixels.

The code to do this is shown below:

turtle.penup()

turtle.setposition(40, 90)

turtle.setheading(90)

turtle.pendown()

turtle.begin_fill()

turtle.forward(10)

turtle.left(90)

turtle.forward(80)

turtle.left(90)

turtle.forward(10)

turtle.left(90)

turtle.forward(80)

turtle.end_fill()

The generated image is shown below:

The code to draw the lower filled quadrant is shown below:

turtle.penup()

turtle.setposition(-40, -90)

turtle.setheading(270)

turtle.pendown()

turtle.begin_fill()

turtle.forward(10)

turtle.left(90)

turtle.forward(80)

turtle.left(90)

turtle.forward(10)

turtle.left(90)

turtle.forward(80)

turtle.end_fill()

The generated image is shown below:

Conclusion

At the end of this section we have successfully drawn the Nya Gyidie symbol.

This post is part of the series: Drawing Adinkra Symbols using Python. The goal is to draw 40 Adinkra symbols using the Python programming language.