SVG with RaphaelJS - Defining Object Boundaries

Welcome to this section of the weekly series SVG with RaphaelJS. In the last section, we covered how to drag and drop a RaphaelJS element. In this section, we shall cover how to detect if two RaphaelJS elements are colliding with each other.

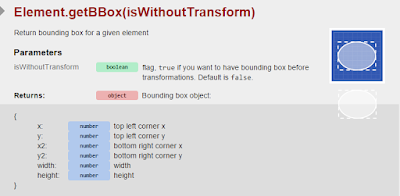
In order to do this, we need to use a bounding box. A bounding box gives us the area around the RaphaelJS element in question. Below is a diagram that shows us this effect.

Getting a bounding box involves using the getBBox command. The parameters returned by this command are the values you see in the above diagram.

We use the same circle element as before. Once we get the bounding box of the circle, we retrieve the x and y values of the circle and use its width and height for the rectangle we want to create.

Remember that the syntax to create a rectangle is:

Paper.rect(x, y, width, height, [r]);

Comparing this to our image above, x and y would be the starting points for the bounding rectangle whlie the width and height would be the width and height of the bounding box respectively.

[r] is an optional parameter that represents the border radius. We don't need it for this case so we won't use it.

The code to do this is given below:

	$(function(){ var paper = Raphael('container', 500, 500);
	// Draw a circle at the left hand side of the viewport
	var circle = paper.circle(100, 250, 50).attr({ 'fill' : 'red', 'stroke-width' : 5 });
	// Get the bounding box of the circle
	var boundingBox = circle.getBBox();
	// Draw the rectangle using components from the bounding box
	paper.rect(boundingBox.x, boundingBox.y, boundingBox.width, boundingBox.height);
	});

The code above produces the output shown below:

Please notice the rectangle around the circle. It shows the bounding box of the circle. An important application of this concept is to check for overlaps of two elements. I will cover that next.

To illustrate this concept, I will draw another circle at the position of x = 400 and y = 250 with the radius = 50. We give the circle we are drawing a colour of blue to differentiate it from our previous circle.

I expect that at this point, you can write the code to do that so I will only show the output.

Lets add our drag methods to the first circle as before however this time in the dragend method, we add an alert method that allows us know if the two circles intersect.

In the dragstart method, we add the toFront() method to first circle to the front of the second circle when dragging starts.

The updated code or the drag functions is shown below:

	$(function(){ var paper = Raphael('container', 500, 500);
	// Draw a circle at the left hand side of the viewport
	var circle = paper.circle(100, 250, 50).attr({ 'fill' : 'red', 'stroke-width' : 5 });
	// Get the bounding box of the circle
	var boundingBox = circle.getBBox();
	// Draw the rectangle using components from the bounding box
	paper.rect(boundingBox.x, boundingBox.y, boundingBox.width, boundingBox.height);
	// Draw a circle at the left hand side of the viewport
	var circle1 = paper.circle(400, 250, 50).attr({ 'fill' : 'blue', 'stroke-width' : 5 });
	circle.drag(dragmove, dragstart, dragend);
	function dragstart(x, y, e){
	this.toFront();
	this.current_transform = this.transform();
	this.attr("fill", "yellow");
	}
	function dragmove(dx, dy, x, y, e){
	this.transform(this.current_transform+'T'+dx+','+dy)
	}
	function dragend(e){
	this.current_transform = this.transform();
	this.attr("fill", "red");
	// Get the bounding box for the target circle
	var targetBBox = circle1.getBBox
	/* Check if the bounding boxes intersect */
	if(Raphael.isBBoxIntersect(boundingBox, targetBBox)){
	alert("The bounding boxes intersect.");
	}
	else{
	alert("The bounding boxes intersect.");
	}
	}
	});

This concept is important if we decide to use SVG for collision detection. Collision detection is an important concept in game development.

This is the tenth part of this series. I have used this first 10 parts to cover basic concepts in using SVG with RaphaelJS. The purpose was to lay the ground work for projects we want to undertake.

From the next section, we shall look at how to create interactive maps. This project will tie in the concepts covered so far.

SVG with RaphaelJS - Drag and Drop in RaphaelJS

Welcome to this section of the weekly series SVG with RaphaelJS.

The drag and drop functionality in RaphaelJS enables us to move elements from one location to another on the RaphaelJS paper.

The documentation is relatively straightforward on how to do this so an example will suffice. We start off by drawing a circle at x = 100 and y = 250 with the radius of 50. The code to do this is given below:

var circle = paper.circle(100, 250, 50).attr({ 'fill' : 'red', 'stroke-width' : 5 });

Notice that we give the circle a fill of red and a stroke-width of 5. This is shown below:

Next we write our dragstart, dragmove and dragend functions and assign them to our circle element.

Our final code is shown below.

	$(function(){ var paper = Raphael('container', 500, 500);
	// Draw a circle at the left hand side of the viewport
	var circle = paper.circle(100, 250, 50).attr({ 'fill' : 'red', 'stroke-width' : 5 });
	circle.drag(dragmove, dragstart, dragend);
	function dragstart(x, y, e){
	this.current_transform = this.transform();
	this.attr("fill", "yellow");
	}
	function dragmove(dx, dy, x, y, e){
	this.transform(this.current_transform+'T'+dx+','+dy)
	}
	function dragend(e){
	this.current_transform = this.transform();
	this.attr("fill", "red");
	}
	});

Note that in the dragstart method when we start dragging the circle, we change its fill colour to yellow.

We also get its current transform first before motion starts. This is because when motion starts, we want to move it in consideration of the transform that it had before motion.

In the dragmove function, we change the transform of the circle in consideration of how it has moved in the x and y directions. The variables dx and dy mean the difference in the motion of the circle along the x and y directions.

You can view the code for this on my dropbox or download the GitHub repository.