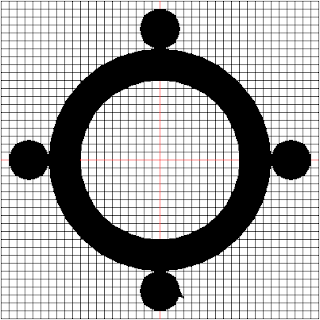
Owia A Repue means "Rising Sun". It is the symbol of progress, renewal, development, warmth, vitality, and energy.
We will use the 5 pixel grid to trace out this image. The image of this is shown below:
The plan to draw this shape is given below:
- Lift up the mouse
- Place the turtle at the left tip of the symbol
- Find the angle and length between the position of the turtle and the next point.
- Draw a line from the left tip to the next point
- Move the turtle to the next point
- Continue steps 3 to 5 until you get to the middle point of the shape
- Draw the rest of the shape
- Fill up the shape
Using Turtle Graphics
We will use the template.py file and rename it to owia.py.
In all the entire shape is made up of 10 lines on the side before the centre line. We shall name the angles and lengths from 1 to 10.
Starting from the left hand side, we have 11 points of interest. Their coordinates are given below:
- (-180, -145)
- (-150, -125)
- (-200, -75)
- (-150, -75)
- (-190, -10)
- (-130, -20)
- (-165, 55)
- (-80, 10)
- (-90, 100)
- (-30, 50)
- (0, 160)
I think its high time to create a function to find the angle between two points. I will call this function angleBetweenPoints.
The code for this function is shown below:
def angleBetweenPoints(x1, y1, x2, y2):
myradians = math.atan2(y2 - y1, x2 - x1)
angle = math.degrees(myradians)
return angle
Now that we have created our function, we have all we need to complete the drawing of this symbol.
To get the length, we reuse the code for the coordinateDistance function which is shown below:
def coordinateDistance(x1, y1, x2, y2):
dx = x1 - x2
dy = y1 - y2
D = math.sqrt((dx * dx) + (dy * dy))
return D
The first step in the algorithm is to lift up the turtle. The code to do this is shown below:
turtle.penup()
Next we move the turtle to the first position on our list which is (-180, -145). The code to do this is shown below:
turtle.setposition(-180, -145)
We find the angle and the length between the first and second position using the code shown below:
angle1 = angleBetweenPoints(-180, -145, -150, -125)
length1 = coordinateDistance(-180, -145, -150, -125)
We do this for the rest of the angles and lengths of the symbol. The code for this is shown below:
angle2 = angleBetweenPoints(-150, -125, -200, -75)
length2 = coordinateDistance(-150, -125, -200, -75)
angle3 = angleBetweenPoints(-200, -75, -150, -75)
length3 = coordinateDistance(-200, -75, -150, -75)
angle4 = angleBetweenPoints(-150, -75, -190, -10)
length4 = coordinateDistance(-150, -75, -190, -10)
angle5 = angleBetweenPoints(-190, -10, -130, -20)
length5 = coordinateDistance(-190, -10, -130, -20)
angle6 = angleBetweenPoints(-130, -20, -165, 55)
length6 = coordinateDistance(-130, -20, -165, 55)
angle7 = angleBetweenPoints(-165, 55, -80, 10)
length7 = coordinateDistance(-165, 55, -80, 10)
angle8 = angleBetweenPoints(-80, 10, -90, 100)
length8 = coordinateDistance(-80, 10, -90, 100)
angle9 = angleBetweenPoints(-90, 100, -30, 50)
length9 = coordinateDistance(-90, 100, -30, 50)
angle10 = angleBetweenPoints(-30, 50, 0, 160)
length10 = coordinateDistance(-30, 50, 0, 160)
Now that we have all the angles we need, we can start drawing the symbol. The code to do this is shown below:
turtle.pendown()
turtle.begin_fill()
turtle.setheading(angle1)
turtle.forward(length1)
turtle.setheading(angle2)
turtle.forward(length2)
turtle.setheading(angle3)
turtle.forward(length3)
turtle.setheading(angle4)
turtle.forward(length4)
turtle.setheading(angle5)
turtle.forward(length5)
turtle.setheading(angle6)
turtle.forward(length6)
turtle.setheading(angle7)
turtle.forward(length7)
turtle.setheading(angle8)
turtle.forward(length8)
turtle.setheading(angle9)
turtle.forward(length9)
turtle.setheading(angle10)
turtle.forward(length10)
turtle.setheading(360 - angle10)
turtle.forward(length10)
turtle.setheading(360 - angle9)
turtle.forward(length9)
turtle.setheading(360 - angle8)
turtle.forward(length8)
turtle.setheading(360 - angle7)
turtle.forward(length7)
turtle.setheading(360 - angle6)
turtle.forward(length6)
turtle.setheading(360 - angle5)
turtle.forward(length5)
turtle.setheading(360 - angle4)
turtle.forward(length4)
turtle.setheading(360 - angle3)
turtle.forward(length3)
turtle.setheading(360 - angle2)
turtle.forward(length2)
turtle.setheading(360 - angle1)
turtle.forward(length1)
turtle.end_fill()
The generated image is shown below:

Conclusion
At the end of this section, we have successfully drawn the Owia A Repue symbol. It is the last hard symbol to draw. From this point on, the rest is easy. 3 more to go.