Nea Ope Se Obedi Hene

Nea Ope Se Obedi Hene means “He who wants to be king”. It is the symbol of symbol of service and leadership.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

The symbol is complex. To draw it, we will need to use some of the techniques that we used to draw the Fawohudie symbol.

The plan to draw the shape is given below:

1. Lift the pen up
2. Set the pen size to 10 pixels
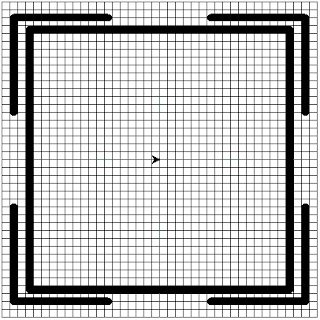
3. Draw the outer 4 bounds
4. Draw the outer square
5. Draw the inner circles
6. Draw the inner V shape
7. Draw the parallel center vertical line

Using Turtle Graphics

We will use the template.py file and rename it to neaopese.py.

The code for steps 1 and 2 are given below:

turtle.penup()

turtle.pensize(10)

The 4 bounds are in the 4 quadrants. We shall draw the 4 bounds starting with the one in the upper left quadrant.

To draw it, we need to move the mouse to its position (-185, 60), set its heading to 90 degrees and move 120 pixels forward. Next we change its heading to 0 degrees and move 120 pixels forward. The code to do this is shown below:

turtle.setposition(-185, 60)

turtle.setheading(90)

turtle.pendown()

turtle.forward(120)

turtle.setheading(0)

turtle.forward(120

To draw the upper right bound, we need to lift up our pen and move the mouse to the position (185, 60). Then we can repeat the steps we used to draw the upper left bound but change the heading to 180 degrees. The code to do this is shown below:

turtle.penup()

turtle.setposition(185, 60)

turtle.setheading(90)

turtle.pendown()

turtle.forward(120)

turtle.setheading(180)

turtle.forward(120)

To draw the lower right bound, we need to lift up our pen and move the mouse to the position (185, -60). Then we can repeat the steps we used to draw the upper left bound but change the heading to 270 degrees. The code to do this is shown below:

turtle.penup()

turtle.setposition(185, -60)

turtle.setheading(270)

turtle.pendown()

turtle.forward(120)

turtle.setheading(180)

turtle.forward(120)

To draw the lower left bound, we need to lift up our pen and move the mouse to the position (-185, -60). Then we can repeat the steps we used to draw the upper left bound but change the heading to 270 degrees. The code to do this is shown below:

turtle.penup()

turtle.setposition(-185, -60)

turtle.setheading(270)

turtle.pendown()

turtle.forward(120)

turtle.setheading(0)

turtle.forward(120)

The generated image is shown below:

To draw the square, we simply use the drawSquare function. The size of the square is 330. So we pass it in as a parameter. The code to do this is shown below:

drawSquare(330)

The generated image is shown below:

To draw the first inner circle, we need to lift up the turtle and move it to the position that is 155 pixels from the center of the circle. Then we draw a circle of radius 155 pixels. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -155)

turtle.pendown()

turtle.circle(155)

The generated image is shown below:

The second circle is 125 pixels from the center of the symbol. We need to lift up the turtle and move it to the position that is 125 pixels from the center of the circle. Then we draw a circle of radius 125 pixels. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -125)

turtle.pendown()

turtle.circle(125)

The generated image is shown below:

To draw the leftward outer line, we need to draw a line from point (0, -155) to (-120, 10). We will use the coordinateDistance function defined earlier using Epa. The function definition is shown below:

def coordinateDistance(x1, y1, x2, y2):

    dx = x1 - x2

    dy = y1 - y2

    D = math.sqrt((dx * dx) + (dy * dy))

    return D

We pass the distance between the two points into a variable called distanceLength. The code to do this is shown below:

distanceLength = coordinateDistance(0, -155, -120, 10)

We also need to find the angle between the two points. The code to do this is shown below:

myradians = math.atan2(10 - (-155), -120 - (0))

upperAngle = math.degrees(myradians)

turtle.setheading(upperAngle)

Once we have the angle between the two points and the length, we need to move the turtle to the point (0, -155) and draw the line. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -155)

turtle.pendown()

turtle.forward(distanceLength)

We now do the same for the right line. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -155)

turtle.setheading(180 -  upperAngle)

turtle.pendown()

turtle.forward(distanceLength)

The generated image is shown below:

To hide the point of intersection between the lines and the inner circle, we need to use a trick. I will move the turtle to the point (0, -140) and draw a triangle to connect points (20, -110) and (-20, -110). The pen colour will be set to white and I shall fill the triangle with a white colour. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -140)

turtle.color(“white”, “white”)

equalSide = coordinateDistance(0, -140, 20, -110)

myradians = math.atan2(-110 - (-140), 20 - (0))

upperAngle = math.degrees(myradians)

turtle.setheading(upperAngle)

turtle.begin_fill()

turtle.pendown()

turtle.forward(equalSide)

turtle.setheading(180)

turtle.forward(40)

turtle.setheading(-upperAngle)

turtle.forward(equalSide)

turtle.end_fill()

The generated image is shown below:

We shall now draw the left inner line. To draw it, we need to first change the pen colour of the mouse to black. Then move it to the position (0, -90). The value of the point on the left side we are trying to get to is (-110, 60). The code to do this is shown below:

turtle.penup()

turtle.pencolor(0, 0, 0)

turtle.setposition(0, -90)

distance = coordinateDistance(0, -90, -110, 60)

myradians = math.atan2(60 - (-90), -110 - (0))

upperAngle = math.degrees(myradians)

turtle.setheading(upperAngle)

turtle.pendown()

turtle.forward(distance)

We need to lift up the pen and move forward by 35 pixels, place the pen down and move forward by 60 pixels. The code to do this is shown below:

turtle.penup()

turtle.forward(35)

turtle.pendown()

turtle.forward(60)

We lift up the turtle and repeat the same sequence for the right. The code to do this is shown below:

turtle.penup()

turtle.setposition(0, -90)

turtle.setheading(180 - upperAngle)

turtle.pendown()

turtle.forward(distance)

turtle.penup()

turtle.forward(35)

turtle.pendown()

turtle.forward(60)

We will comment out the drawHorizontalLine and drawVerticalLine functions and see our creation in all its glory.

The generated image is shown below:

Conclusion

This was one of the harder symbols to draw. But at the end, we made it.