Mframadan

Mframadan means "wind resistant house". It is the symbol of symbol of fortitude and readiness to face life's vicissitudes.

This symbol suggests a reinforced or well-built home one built to withstand windy and treacherous conditions. It reflects in Asante history a clause in the unwritten constitutution of the Golden Stool.

Oral acocunts say that according to that clause, mud houses in Kumasi must be reinforced with turf. This reinforcing would cause the house to be sturdier and resistant to unfavorable weather conditions.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

The plan to draw this shape is shown below:

1. Lift the turtle
2. Set the pen size to 10
3. Draw the outer square
4. Draw the inner square
5. Draw the diagonal lines
6. Draw the 4 remaining lines at the bottom
7. Draw the 4 remaining lines at the top

Using Turtle Graphics

We will use the template.py file and rename it to mframadan.py.

The code for steps 1 and 2 is given below:

turtle.penup()

turtle.pensize(15)

The outer square of the symbol is to be drawn first. Thankfully, we have the drawSquare function. Its length is 380 pixels. We use the drawSquare function to draw this shape by entering 380 as a parameter. The code for this is shown below:

drawSquare(380)

The generated image is shown below:

To draw the inner square, we also need to use the drawSquare function. The length of the square is 300 pixels. We use the drawSquare function to draw this shape by entering 300 as a parameter. The code to do this is shown below:

drawSquare(300)

The generated image is shown below:

To draw the diagonals that start at the lower left and move to the right quadrant, we must first get their positions.

To draw the lower line, we must move the turtle to its position and set is heading to 45 degrees. Then we move the turtle forward. The code to do this is shown below:

turtle.setposition(-110, -150)
turtle.setheading(45)
turtle.pendown()
turtle.forward(365)

The generated image is shown below:

Next we draw the upper left lower line. To do this, we move it to a position that is (-150, -110). We set the heading of the turtle to 45 degrees and we draw a line of length 365. The code to do this is shown below:

turtle.penup()
turtle.setposition(-150, -110)
turtle.setheading(45)
turtle.pendown()
turtle.forward(365)

The generated image is shown below:

Now we shall do the same thing for the right lines. The coordinates for the lower right lower line is (110, -150). Now that we know that, we shall repeat the steps we used to draw its counterpart only that its heading will be 135 degrees. The code to do this is shown below:

turtle.penup()
turtle.setposition(110, -150)
turtle.setheading(135)
turtle.pendown()
turtle.forward(365)

We just do the same thing for the upper right lower line. Its coordinates are (150, -110). The code to draw it is given below:

Next we draw the bottom lines. The first bottom line starts at the position (-90, -130) and extends to the position (90, -130). The distance between the lines is 180 pixels. The code for this is shown below:

turtle.penup()
turtle.setposition(-90, -130)
turtle.setheading(0)
turtle.pendown()
turtle.forward(180)

The generated image is shown below:

The coordinates for the second bottom line are at (-70, -110). We need to draw a line of length 140. The code to do this is shown below:

turtle.penup()
turtle.setposition(-70, -110)
turtle.setheading(0)
turtle.pendown()
turtle.forward(140)

The generated image is shown below:

The coordinates for the third bottom line are at (-50, -90). We need to draw a line of length 100. The code to do this is shown below:

turtle.penup()
turtle.setposition(-50, -90)
turtle.setheading(0)
turtle.pendown()
turtle.forward(100)

The generated image is shown below:

The coordinates for the third bottom line are at (-30, -70). We need to draw a line of length 60. The code to do this is shown below:

turtle.penup()
turtle.setposition(-30, -70)
turtle.setheading(0)
turtle.pendown()
turtle.forward(60)

The generated image is shown below:

To draw the four top lines, we only need to reverse the along the y axis. So, the code to draw the four top lines is shown below:

turtle.penup()
turtle.setposition(-90, 130)
turtle.setheading(0)
turtle.pendown()
turtle.forward(180)

turtle.penup()
turtle.setposition(-70, 110)
turtle.setheading(0)
turtle.pendown()
turtle.forward(140)

turtle.penup()
turtle.setposition(-50, 90)
turtle.setheading(0)
turtle.pendown()
turtle.forward(100)

turtle.penup()
turtle.setposition(-30, 70)
turtle.setheading(0)
turtle.pendown()
turtle.forward(60)

The final shape is now shown below:

Conclusion

We have used Python Turtle Graphics to draw the Mframadan symbol. Now that the meaning is clear, I realize that the lines we drew last represents the rafters.

The entire symbol is symbolic of a roof viewed from above.

Me-Ware-Wo

Me-Ware-Wo means "I shall marry you". It is the symbol of commitment and perseverance.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

The plan to draw this shape is shown below:

1. Lift the turtle
2. Set the pen size to 20 pixels
3. Move the turtle to the position (-90, 10)
4. Place the pen down
5. Draw a circle of radius 80 pixels
6. Set the heading of the turtle to 90 degrees
7. Move forward by 50 pixels
8. Change the heading of the turtle to 0 degrees
9. Change the pen size to 1 pixel
10. Draw a filled circle of radius 30 pixels
11. Lift the pen
12. Move the turtle to the position (90, 10)
13. Set the pen size to 20 pixels
14. Repeat steps 4 to 10
15. Lift the pen
16. Move the turtle to the position (90, -170)
17. Set the pen size to 20 pixels
18. Repeat steps 4 to 10
19. Lift the pen
20. Move the turtle to the position (-90, -170)
21. Set the pen size to 20 pixels
22. Repeat steps 4 to 10

Using Turtle Graphics

We will use the template.py file and rename it to mewarewo.py.

The code for steps 1 - 5 is given below:

turtle.penup()

turtle.pensize(20)

turtle.setposition(-90, 10)

turtle.pendown()

turtle.circle(80)

The generated image is shown below:

The code for steps 6 to 10 is given below:

turtle.setheading(90)

turtle.forward(50)

turtle.setheading(0)

turtle.pensize(1)

turtle.begin_fill()

turtle.circle(30)

turtle.end_fill()

The generated image is shown below:

Steps 14, 18 and 22 are repeated. This would be a good candidate for a function. So we create a function called draw_quarter_symbol and place it just after drawVertical function.

The code for the draw_quarter_symbol is shown below:

def draw_quarter_symbol():

    turtle.pendown()

    turtle.circle(80)

    turtle.setheading(90)

    turtle.forward(50)

    turtle.setheading(0)

    turtle.pensize(1)

    turtle.begin_fill()

    turtle.circle(30)

    turtle.end_fill()

This step we have carried out is called refactoring. The code that draws our symbol now becomes:

turtle.penup()

turtle.pensize(20)

turtle.setposition(-90, 10)

draw_quarter_symbol()

Run the above code and test it. The program runs as expected. To draw the rest of the symbol, you only need to copy and paste the code above 3 more times. Then you change the position you move your turtle to.

The code for our program now becomes:

turtle.penup()

turtle.pensize(20)

turtle.setposition(-90, 10)

draw_quarter_symbol()

turtle.penup()

turtle.pensize(20)

turtle.setposition(90, 10)

draw_quarter_symbol()

turtle.penup()

turtle.pensize(20)

turtle.setposition(90, -170)

draw_quarter_symbol()

turtle.penup()

turtle.pensize(20)

turtle.setposition(-90, -170)

draw_quarter_symbol()

The generated image is shown below:

Conclusion

At the end of this section, we have used the Python language to draw the Adinkra symbol Me Ware Wo.

Kuntinkantan

Kuntinkantan means “puffed up extravagance”. It is the symbol of arrogance.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

This shape is easy to draw. It consists only of circles. It is a made up of a central circle that encloses the other 4 circles.

The plan to draw this shape is shown below:

1. Lift the turtle
2. Set the pen size to 20 pixels
3. Move the turtle to the position (0, -90)
4. Place the pen down
5. Draw a circle of radius 90 pixels
6. Lift up the pen
7. Move the turtle to the position (-90, 10)
8. Place the pen down
9. Draw a circle of radius 80 pixels
10. Lift up the pen
11. Move the turtle to the position (90, 10)
12. Place the pen down
13. Draw a circle of radius 80 pixels
14. Lift up the pen
15. Move the turtle to the position (-90, -170)
16. Place the pen down
17. Draw a circle of radius 80 pixels
18. Lift up the pen
19. Move the turtle to the position (90, -170)
20. Place the pen down
21. Draw a circle of radius 80 pixels

Using Turtle Graphics

We will use the template.py file and rename it to kuntinkantan.py.

The code for steps 1 to 5 is shown below:

turtle.penup()

turtle.pensize(20)

turtle.setposition(0, -90)

turtle.pendown()

turtle.circle(90)

The generated image is shown below:

The code for steps 6 to 9 is given below:

turtle.penup()

turtle.setposition(-90, 10)

turtle.pendown()

turtle.circle(80)

The generated image is shown below:

The code for steps 10 to 13 is given below:

turtle.penup()

turtle.setposition(90, 10)

turtle.pendown()

turtle.circle(80)

The generated image is shown below:

The code for steps 14 to 17 is shown below:

turtle.penup()

turtle.setposition(-90, -170)

turtle.pendown()

turtle.circle(80)

The generated image is shown below:

The code for steps 18 to 21

turtle.penup()

turtle.setposition(90, -170)

turtle.pendown()

turtle.circle(80)

The generated image is shown below:

Conclusion

At the end of this section, we have successfully used Python turtle to draw the Kuntinkantan symbol.

If you look critically at this symbol, you would see a possible inspiration for the Olympics symbol.

Kete-Pa

Kete-Pa means "good bed". It is the symbol of a good marriage. It is derived from the expression that a woman who has a good marriage is said to sleep on a good bed.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

This shape is easy to draw. It consists only of straight lines. This lines are horizontal and vertical.

The easiest way to draw this symbol is to use a loop. We will draw the horizontal symbols first and the vertical symbols next.

Thankfully in our template we already have functions that can do this. They are the drawHorizontalLine and drawVerticalLine functions.

The plan to draw this symbol is shown below:

1. Set the pen size to 10 pixels
2. Use the drawHorizontalLine function with 11 divisions
3. Use the drawVerticalLine function with 11 divisions

Using Turtle Graphics

We will use the template.py file and rename it to ketepa.py.

The code for step 1 is given below:

turtle.pensize(10)

The code for step 2 is given below:

drawHorizontalLine(330, 11)

The code for step 3 is given below:

drawVerticalLine(330, 11)

The generated image is shown below:

Conclusion

At the end of this section, we have successfully used Python turtle to draw the Kete-Pa symbol.

This is one of the easiest symbol to draw because it is made up of lines.

Thankfully, we have no need to do any coding because we simply needed to use the functions in our template file.

Hwemudua

Hwemudua means "measuring stick". It is the symbol of examination and quality control. This symbol stresses the need to strive for the best quality, whether in production of goods or in human endeavors.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

This shape is easy to draw. It consists only of straight lines. This lines are horizontal and vertical.

The width of the blocks is taken to be 4 squares. With this information, we can draw the entire shape. We will draw the horizontal lines first.

The plan to draw this shape is given below:

1. Lift the turtle
2. Set the pen size to 40 pixels
3. Move the turtle to the position that is (-160. -170)
4. Place the pen down
5. Move the turtle forward by 320 pixels
6. Lift up the pen
7. Move the turtle to the position that is (-120. 170)
8. Place the pen down
9. Move the turtle forward by 240 pixels
10. Lift up the pen
11. Move the pen to the point that is (-170. -80)
12. Set the heading of the pen to 90 degrees
13. Place the pen down
14. Move 130 pixels forward
15. Set the heading of the pen to 0 degrees
16. Move the turtle forward by 340 pixels
17. Set the heading of the pen to 270 degrees
18. Move 130 pixels forward
19. Lift up the pen
20. Move the pen to the position (-80, -170)
21. Set the heading of the turtle to 90 degrees
22. Place the pen down
23. Move forward by 200 pixels
24. Lift up the pen
25. Move the pen to the position (-80, 0)
26. Set the heading of the turtle to 90 degrees
27. Place the pen down
28. Move forward by 250 pixels
29. Lift up the pen
30. Move the pen to the position (80, -170)
31. Set the heading of the turtle to 90 degrees
32. Place the pen down
33. Move forward by 200 pixels

Using Turtle Graphics

We will use the template.py file and rename it to hwemudua.py. 

The code for steps 1 to 5 is shown below:

turtle.penup()

turtle.pensize(40)

turtle.setposition(-160, -170)

turtle.pendown()

turtle.forward(320)

The generated image is shown below:

The code for steps 6 to 9 are given below:

turtle.penup()
turtle.setposition(-160, 170)
turtle.pendown()
turtle.forward(240)

The generated image is shown below:

The next part of the symbol to be drawn is the upside down U shape. To draw it, we would need to first move the cursor to the point where (-170, -80).

The steps 10 to 18 are given in code as shown below:

turtle.penup()
turtle.setposition(-170, -80)
turtle.setheading(90)
turtle.pendown()
turtle.forward(130)
turtle.setheading(0)
turtle.forward(340)
turtle.setheading(270)
turtle.forward(130)

The generated image is shown below:

To complete this symbol, now all we have to do is draw the vertical lines. We start from the left of the shape.
The steps 19 to 23 are given in code shown below:

turtle.penup()
turtle.setposition(-80, -170)
turtle.setheading(90)
turtle.pendown()
turtle.forward(200)

The generated image is shown below:

The code for steps 24 to 28 is given below:

turtle.penup()
turtle.setposition(0, -80)
turtle.setheading(90)
turtle.pendown()
turtle.forward(250)

The generated image is shown below:

The code for the steps 29 to 33 is given below:

turtle.penup()
turtle.setposition(80, -170)
turtle.setheading(90)
turtle.pendown()
turtle.forward(200)

The generated image is shown below:

Conclusion

At the end of this section, we have successfully used Python turtle to draw the Hwemudua symbol.

This is one of the easiest symbol to draw because it is made up of lines.

Fofoo

Fofoo means "yellow flowered plant". It is the symbol of jealousy and envy. When the fofo's petals drop, they turn into black spiky-like seeds. The Akan liken the nature of this plant to a jealous person.

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

This symbol consists of lines and circles. The inner circle is of a radius of 3 squares. The outer rim is of a width of 3 squares. The line from the rim to the outer circle is of 4 squares in width. Its length starts from around the point where the distance from the centre is 5 squares. It stretches up to the point which is 13 squares from the centre of the circle. The line is closed up by a filled circle. Its radius is 3 squares.

The plan to draw this symbol is as follows:

1. Lift the turtle
2. Move it to the position that is 5 squares from the centre of the symbol
3. Place the turtle down
4. Set its pensize to 4 squares
5. Draw a circle of a radius of 5 squares
6. Lift up the pen
7. Move it back to the centre of the symbol which is at the origin
8. Set the pensize to 3 squares
9. Set the heading of the turtle to 90 degrees
10. Move to the position that is 5 squares from the centre of the circle in the direction of the heading of the turtle
11. Place the turtle down
12. Draw a line by moving forward by 8 squares
13. Set the orientation of the turtle based on the formula (heading - 90)
14. Set the pensize to 1
15. Draw a filled circle from the point the line stops
16. Go back to step 6 but each time you get to step 9, increase the heading by 40 until you get to 410

Using Turtle Graphics

We will use the template.py file and rename it to fofoo.py. The size of each square on our grid is 10 pixels. We shall use this as our multiplication factor.

From our first step, we need to lift up the pen. The code to do this is shown below:

turtle.penup()

To move the turtle to the point that is 5 squares from the center of the figure, we want to move it to the location that is (0, -5). Due to the multiplication factor of 10, this will now become (0, -50). The code to do this is given below:

turtle.setposition(0, -50)

To place the turtle down. The code to place the turtle down is shown below:

turtle.pendown()

To set the pensize to 4 squares, we will multiply this by 10 to get 40. The code to do this is shown below:

turtle.pensize(40)

We need to draw a circle of radius 5 squares. We use our multiplication factor and the value becomes 50. The code to do this is shown below:

turtle.circle(50)

The image that is generated is shown below:

Steps 6 to 12 are summarized by the steps shown below:

turtle.penup()
turtle.home()
turtle.pensize(30)
turtle.setheading(90)
turtle.forward(50)
turtle.pendown()
turtle.forward(80)

The generated image is shown below:

The code for steps 13, 14 and 15 are given below:

turtle.setheading(0)
turtle.pensize(1)
turtle.begin_fill()
turtle.circle(30)
turtle.end_fill()

The generated image is shown below:

Step 16 indicates that this is a loop. So we go back to step 6.

Now it would be easier to just use a simple while loop. So delete all the code for step 6 to step 15 and just enter this:
heading = 90

while (heading <= 410):
    turtle.penup()
    turtle.home()
    turtle.pensize(30)
    turtle.setheading(heading)
    turtle.forward(50)
    turtle.pendown()
    turtle.forward(80)
    turtle.setheading(heading - 90)
    turtle.pensize(1)
    turtle.begin_fill()
    turtle.circle(30)
    turtle.end_fill()
    heading = heading + 40

If you look carefully, you will see all the steps from steps 6 to 16 in this code. The only thing different about this code is the introduction of a variable called heading.

The generated image is shown below:

Conclusion

At the end of this section, we have successfully used Python turtle to draw the Fofoo symbol.

The use of a loop made the drawing of this symbol easier than if we had drawn each part individually.

Fawohudie

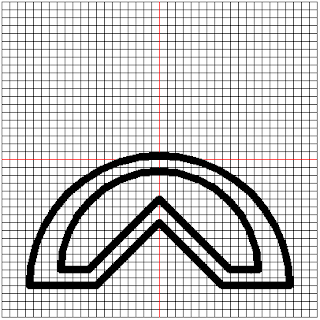
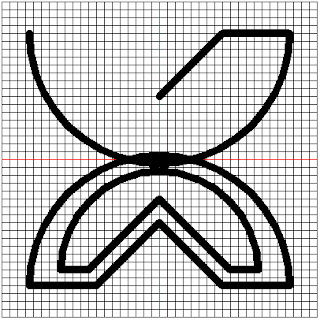
Fawohudie means "Independence". It is the symbol of independence, freedom and emancipation. 

We will use the 5 pixel grid to trace out this image. The image of this is shown below:

This symbol consists of semi-circles and straight lines. The outermost circles intersect with each other however, their point of intersection is erased out slightly. The entire shape symmetric. We will start with the lower circle. 

The plan to draw this shape is as follows:

1. Lift the turtle
2. Move the turtle to the position at the right edge of the circle
3. Place the turtle down
4. Draw the semi-circle
5. Set the heading of the turtle to 0 degrees
6. Draw the line down to the point where it moves up
7. Draw the line up to the origin point
8. Draw the line down to the point where it flattens
9. Draw the line to the other part of the semi-circle
10. Use the other steps from 1 to 9 to draw the inner circle and its own lines
11. Repeat the above steps from 1 to 9 to draw the outer circle for the upper part
12. Repeat the above steps from 1 to 9 to draw the inner circle for the upper part
13. Draw the that erases the point of intersection between the two lines

Using Turtle Graphics

We will use the template.py file and rename it to fawohudie.py. The size of each square on our grid is 10 pixels. We shall use this as our multiplication factor.

From step 1 of our plan, we need to lift we need to lift the pen. The code to do this is shown below:

turtle.penup()

The point at the right edge of the circle is at the coordinates (16.5, -16). Using a scale factor of 10, our coordinates now become (165, -160).

The code to move our turtle to this position is:

turtle.setposition(165, -160)

We need to set the heading of our turtle to 90 degrees. The code to do this is shown below:

turtle.setheading(90)

We will increase the pensize of our turtle to 10 pixels. The code to do this is shown below:

turtle.pensize(10)

For our third step, we need to place the pen down so that the turtle can begin drawing. The code to do this is shown below:

turtle.pendown()

The code to draw the semi-circle is shown below:

turtle.circle(165, 180)

The generated image is shown below:

Now we set the heading of the turtle to 0 degrees. The code to do this is shown below:

turtle.setheading(0)

The coordinates of the point where the line moves up are (-80, -160). The distance from the current point where the turtle is to this point is 85 pixels. So we can move the turtle forward by 85 pixels. The code to do this is shown below:

turtle.forward(85)

The image generated is shown below:

To draw a line up to the origin point, we need to find the distance from where the turtle is to the origin point. The coordinates of the point where the turtle is (-80, -160) and the coordinates of the origin point is (-80, 0). We already know that the angle between the two points is 45 degrees.

We will use the coordinateDistance function that we used to draw the Epa symbol. The function definition is given below:

def coordinateDistance(x1, y1, x2, y2):

dx = x1 - x2

dy = y1 - y2

D = math.sqrt((dx * dx) + (dy * dy))

return D

The code to use this function for our case is shown below:

outerLine = coordinateDistance(-80, -160, 0, -80)

The outerLine variable will be used throughout this program to draw the other outer lines.

Now we set the heading of our shape to 45 degrees. The code to do this is shown below:

turtle.setheading(45)

Now we move forward by the length of the outerLine. The code to do this is shown below:

turtle.forward(outerLine)

The generated image is shown below:

Now that we have the variable outerLine and we know that the angle is 45 degrees, we can complete the outer shape.

We need to draw the line from the point where it currently is to the point where it rejoins the flat part of the shape. To do this, our heading needs to be 315 degrees and we need to move forward by the length of the outerLine. The code to do this is shown below:

turtle.setheading(315)

turtle.forward(outerLine)

The generated image is now:

All we have to do now is to set the heading of the turtle to 0 degrees and make the turtle move forward by 85 pixels. The code to do this is shown below:

turtle.setheading(0)

turtle.forward(85)

The generated image is shown below:

At this stage, the outer part of the lower part of our symbol is done. We will use the same steps we have followed to draw the inner part or the lower part of our symbol.

We repeat the steps we used to draw the outer part to draw the inner part. The coordinates of the point in the inner part of the shape is (125, -140). So we can lift up the pen and move the turtle to the point (125, -140). The code to do this is shown below:

turtle.penup()

turtle.setposition(125, -140)

Now we place the pen down and set it heading to 90 degrees. The code to do this is shown below:

turtle.setheading(90)

turtle.pendown()

Now we can draw a semi-circle of radius 125. The code to do this is shown below:

turtle.circle(125, 180)

Now we need to draw the inner left line. The way to do this will be to set the heading of your turtle to 0 degrees and move in by 35 pixels.

The code that does this is shown below:

turtle.setheading(0)

turtle.forward(35)

The image generated is shown below:

innerLine = coordinateDistance(-90, -140, 0, -50)

turtle.setheading(45)

turtle.forward(innerLine)

The generated image is shown below:

We repeat the steps from step 8 of our algorithm. The code to do this is shown below:

turtle.setheading(315)

turtle.forward(innerLine)

The generated image is shown below:

To complete the lower part of this shape, we need to set the heading of the turtle back to 0 degrees and move forward by 35 pixels. The code to do this is shown below:

turtle.setheading(0)

turtle.forward(35)

The generated image is shown below:

The lower part of the symbol is complete. Now we can start drawing the upper part of our symbol. 

To draw the upper part of this symbol, we repeat the steps we have taken so far and do them for the upper part of this symbol. 

The first step is to lift up the turtle. The code to do this is shown below:

turtle.penup()

We now move the turtle to the upper left hand side. The code to do this is given below:

turtle.setposition(-165, 160)

Next we set the heading of the turtle to 270 degrees. The code to achieve this is given below:

turtle.setheading(270)

The pen is now placed down and we draw a semi-circle. The code that does this is shown below:

Now we set the heading to 180 degrees and we move to the left by 85 pixels. The code that does this is given below:

turtle.setheading(180)

turtle.forward(85)

The image generated is shown below:

The distance up to the line where the origin point is has already been obtained. It is the variable outerLine. The angle between the two points is 45. So we can set the heading and move forward by the value of the outerLine. The code to do this is shown below:

turtle.setheading(225)

turtle.forward(outerLine)

The generated image is shown below:

We need to draw the line from the point where the turtle is to where it rejoins the flat part of the shape. The code to do this is given below:

turtle.setheading(135)

turtle.forward(outerLine)

The generated image is shown below:

To complete the outer part of our shape, we need to draw the line back to our starting position. The code to do this is shown below:

turtle.setheading(180)

turtle.forward(85)

Our generated image now becomes:

To draw the inner upper part of the symbol, we need to lift up the pen and move it to the point (-125, 140). The heading must also be set to 270 degrees. We then put down the pen and draw a circle of radius 125. The code to do this is shown below:

turtle.penup()

turtle.setposition(-125, 140)

turtle.setheading(270)

turtle.pendown()

turtle.circle(125, 180)

The generated image is shown below:

To draw the inner right line, we need to set the heading to 180 degrees and move in by 35 pixels. The code to do this is given below:

turtle.setheading(180)

turtle.forward(35)

The generated image is shown below:

We know that the length from where the turtle currently is the innerLine variable. We set the heading to 225 degrees.

The code to do this is shown below:

turtle.setheading(225)

turtle.forward(innerLine)

The generated image is shown below:

Now we draw a line back to where the straight line will be drawn to. The code to do this is shown below:

turtle.setheading(135)

turtle.forward(innerLine)

The generated image is shown below:

The drawing will be completed by drawing line to the starting point. To do this, we set the heading of our turtle to 180 degrees and draw a line to our starting point.

The code to do this is shown below:

turtle.setheading(180)

turtle.forward(35)

The image generated is shown below:

All that is left is to clean up the part where the outer circles intersect. To do this, we must move the turtle to where the turtles first intersect. This position is at (-50, 0), set the heading of the turtle to 0 degrees, change the colour of the pen to white, increase the pensize to 20 pixels and draw a line that is 100 pixels in length.

The code to do this is shown below:

turtle.penup()

turtle.setposition(-40, 0)

turtle.setheading(0)

turtle.pendown()

turtle.pencolor(255, 255, 255)

turtle.pensize(20)

turtle.forward(80)

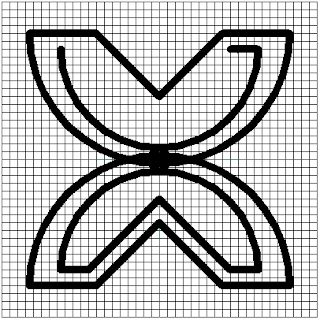
To draw the final image, I placed a comment on the call to the drawHorizontalLine(400, 40) and drawVerticalLine(400, 40) functions. The final image is thus:

The inner arrow is the turtle. Beyond that, this shape is done.

Summary

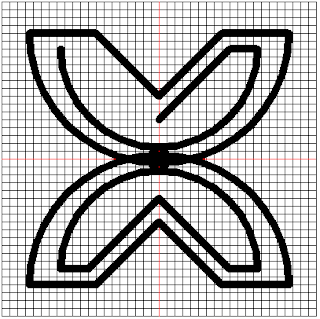
At the end of this section, we have successfully used Python turtle to draw the Fawohudie symbol. I will admit that the final output isn’t perfect but the basic symbol has been drawn.